Work in progress …
Beginning to read again the „The Last Theorem“ I was confrontated with Fermat. Not for the first time. As an enthusiastic never-ever-mathematician I, of course, could not resist to eye on this problem. That story where Fermat said, that a2 + b2 = c2 only works in this power and not for power of 3. As far as I understood the basics.
The formula is expressing the relation between the three lines in two dimension forming a right triangle. And only for this type of triangle. The maths are based on geometry and the explicite form of a right triangle, which requires at least two dimensions.
Usually, as far as I have seen, and I have not seen almost something, Fermat is connected to number theory. But I ask myself, is it really a problem of number theory, sure also, but where is the source. And the source, as far as I understand is geometry and dimension.
For me, as a stupid, it seems that the power of two is the equivalence for the geometric relations of the dimension n = 2. Ignoring for the moment, that it requires a special triangle type. So I tried to reduce. The dimension. Getting to the source.
What if I think a radical triangle with two angles zero and one angle 180o? A line.
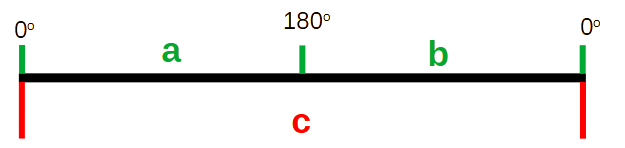
With a split point somewhere up the line. Middle is a very special situation. Results in an equiliteral or isosceles triangle if extending the dimension. Only one right triangle is possible if the split point is in the middle (45o, 45o, 90o).
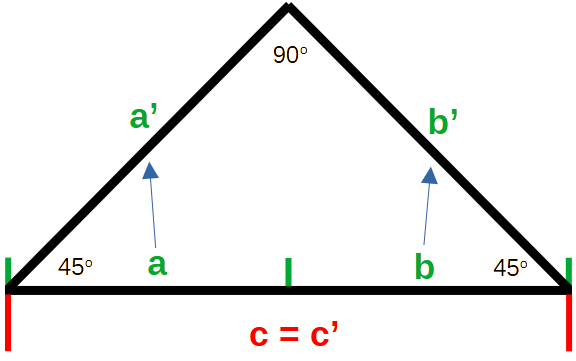
But we end up with a line split somewhere, where a + b = c is true, but a2 + b2 = c2 only if a and b are zero or c is zero. According to current rules in the first dimension. Extending to the next dimension is just lifting a and b by an defined angle and closing the gap. So we get a‘ and b‘ not equal to a and b, whereas c is not changing.
So I could assume:
a1 + b1 = c1
a2 + b2 = c2
a3 + b3 = c3
Looks like a promising pattern. If I ignore forms and dimensions. Concentrated on numbers only.
But thinking in dimensions, shapes and geometry it makes only sense for the first and very limited for the second dimension. And only for the special case of a right triangle. Or a shape I could cut into right triangles. The third dimension usually needs more points to describe the form and relation.
So the question is, do there exist three dimensional shapes using a right triangle with always equal values for all a, b and c representations of the right triangle used to create the shape? A cone could possibly fulfill this requirement.
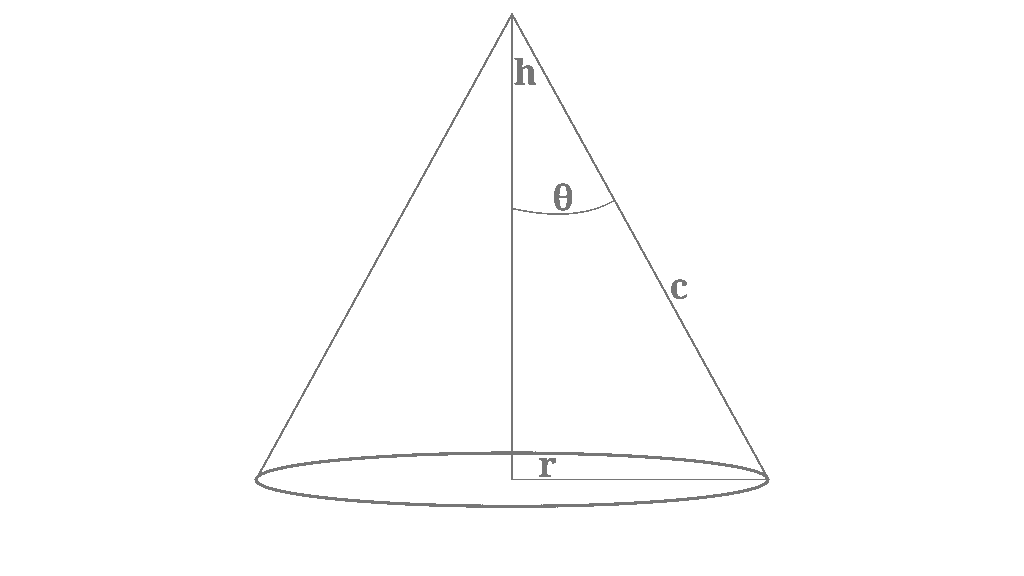
But will a3 + b3 = c3 or r3 + h3 = c3 work on specific shapes and give us a useful information?
As the right triangle is a special case of triangle in the second dimension it is highly to expect that only a even more special shape in the third dimension can give a useful and correct result. It is imho very possible that if, the result is related to the volume, not to the length of lines.
But more I think that the formula will need a transformation to represent correctly the dimension. From a quick test I have seen that at least mathematically
(a2 + b2)3 = c2*3
gives some valid mathematical results. If they make sense in geometry I don’t know yet. Only a short test with simple integers for a and b. It seems also to work for higher dimensions
(a2 + b2)n = c2*n
So one could argument, that the transformation of the formula to the next dimension or power is wrong and it therefore can’t work, if you elevate the relation between a, b and c to the next dimension based on special triangle shapes.
And correct transformation steps would be
an + bn = cn where n > 0 and n < 3
(a2 + b2)n = c2*n where n > 2
Reason: Beginning with the third dimension, I have to treat two dimensional shapes as an object, so I must treat a2 + b2 as an object. Raising the power simply on a and b destroys the object and its sum relation.
From number theory this would probably lead to the idea, that any or most sum relations and equations where power/dimension is involved can’t be splitted if you want to raise it to a higher power by simply raising the power. The power to raise has to be used on the sum, not on the summands. Probably there is already an algebra rule that would be broken by only raising the power of the summands and the equation. Should search for it.
Still thinking …
Any input use mail toent with base URL of this website. Minimum intellect required to fiddle out the mail address.

